Final Summary Data Structure
Final Summary Data Structure
Nama : Nicholas Anderson
NIM : 2301861043
Kelas : CB01
Dosen : Henry Chong (D4460) & Ferdinand Ariandy Luwinda (D4522)
Linked List

Nama : Nicholas Anderson
NIM : 2301861043
Kelas : CB01
Dosen : Henry Chong (D4460) & Ferdinand Ariandy Luwinda (D4522)
Linked List
Linked list atau dikenal juga dengan sebutan senarai berantai adalah struktur data yang terdiri dari urutan record data dimana setiap record memliki field yang menyimoan alamat/ referensi dari record selanjutnya (dalam urutan) elemen data yang dihubungkan dengan link pada linked list disebut Node.
Biasanya didalam suatu linked list, terdapat istilah head and tail.
- Head adalah elemen yang berada pada posisi pertama dalam suatu linked list
- Tail adalah element yang berada pada posisis terakhir dalam suatu linked list
Apa perbedaan antara Array dan Linked List ?

Ada beberapa jenis Linked List :
- Single Linked List
Merupakan linked list yang hanya menggunakan 1 pointer saja, dimana pointer menunjuk pada node selanjutnya dan tail menunjuk ke null.Contoh ilustrasi :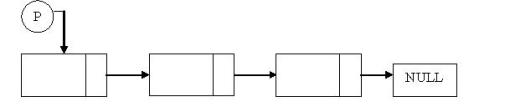
Contoh Codingan :struct Mahasiswa{char nama[25];
char NIM[10];
int usia;
struct Mahasiswa *next;
}*head,*tail; - Double Linked List
Merupakan linked list yang menggunakan 2 buah pointer, yang dimana pointer pertama untuk menunjuk node selanjutnya sedangkan yang kedua untuk menunjuk node sebelumnya. tail juga menunjuk ke null.
Contoh ilustrasi :
Contoh Codingan :struct Mahasiswa{char nama[25];
char NIM[10];
int usia;
struct Mahasiswa *next,*prev;
}*head,*tail; - Single Circular Linked List
Merupakan linked list yang pointernya menunjuk pada dirinya sendiri, dan tailnya menujuk pada node terdepan(head).
Contoh ilustrasi :
- Double Circular Linked List
Merupakan linked list yang memeliki 2 pointer yang menujuk pada dirinya sendiri, dan tailnya juga menunjuk pada node terdepan(head).
Contoh ilustrasi :
https://kuliahinformatika.wordpress.com/2010/01/21/linked-list-definisi-node-linked-list-single-linked-list-double-linked-list-circular-linked-list/
https://bocahngoding.blogspot.com/2017/12/1-array-dan-single-linked-list.html
https://bocahngoding.blogspot.com/2017/12/1-array-dan-single-linked-list.html
Insert dan Delete pada Linked List
Sumber :
https://socs.binus.ac.id/2017/03/15/single-linked-list/
https://socs.binus.ac.id/2017/03/15/doubly-linked-list/
PPT Binus(Stack & Queue)
Untuk delete pada AVL Tree hampir sama dengan Delete pada BST, tapi karena untuk menghapus node juga dapat menyebabkan tree menjadi tidak seimbang, jadi untuk itu pada Delete juga digunakan konsep Single Rotation dan Double Rotation.
Sumber :
http://dinda-dinho.blogspot.com/2013/06/pengertian-dan-konsep-avl-tree.html
PPT Binus AVL Tree
A. Insert pada linked list
merupakan operasi yg dilakukan untuk meinsert data pada suatu linked list.
merupakan operasi yg dilakukan untuk meinsert data pada suatu linked list.
- Insert pada single linked list
- Push depan -> memasukkan data dari depan.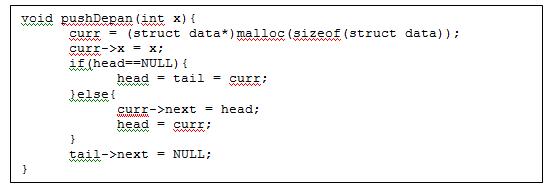
- Push belakang -> memasukkan data dari belakang.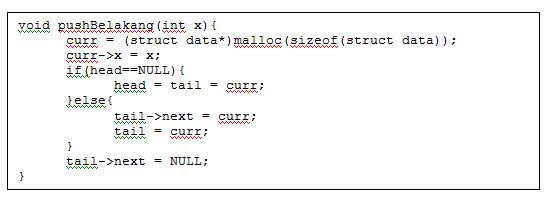
- Insert pada double linked list
- Push depan -> memasukkan data dari depan, tetapi menggunakan 2 pointer.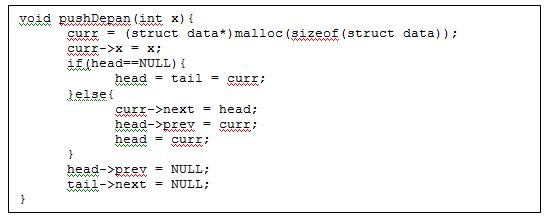
- Push belakang -> memasukkan data dari belakang, tetapi menggunakan 2 pointer.
B. Delete pada linked list
merupakan operasi yg dilakukan untuk menghapus data pada suatu linked list.
merupakan operasi yg dilakukan untuk menghapus data pada suatu linked list.
- Delete pada single linked list
- Pop depan -> menghapus data dari depan.
- Pop belakang -> menghapus data dari belakang.
- Delete pada double linked list
- Pop depan -> menghapus data dari depan, tetapi menggunakan 2 pointer.
- Pop belakang -> menghapus data dari belakang, tetapi menggunakan 2 pointer.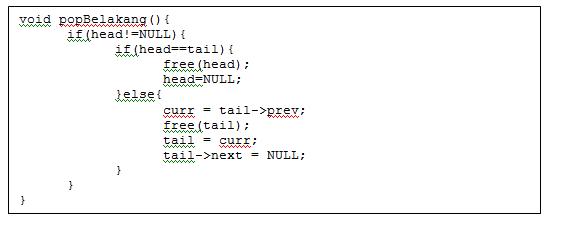
C. Stack
merupakan sebuah tumpukan, yg dimana data yang terakhir masuk akan keluar
duluan(LIFO -> Last In First Out). Stack merupakan gabungan dari push depan
dan pop depan.
D. Queue
merupakan sebuah antrian, yang dimana data yang pertama masuk akan keluar
duluan(FIFO -> First In First Out). Queue merupakan gabungan dari push belakang
dan pop depan.
Sumber :
https://socs.binus.ac.id/2017/03/15/single-linked-list/
https://socs.binus.ac.id/2017/03/15/doubly-linked-list/
PPT Binus(Stack & Queue)
HASHING
merupakan metode untuk menyimpan data dalam sebuah array agar penyimpanan data, pencarian data, penambahan data, dan penghapusan data dapat dilakukan dengan cepat. Ide dasarnya adalah menghitung posisi recordyang dicari dalam array, bukan membandingkan record dengan isi pada array. Fungsi yang mengembalikan nilai atau kunci disebut fungsi hash (hashfunction) dan array yang digunakan disebut tabel hash (hash table). Hash tablemenggunakan struktur data array asosiatif yang mengasosiasikan recorddengan sebuah field kunci unik berupa bilangan (hash) yang merupakan representasi dari record tersebut.
Function-function yang terdapat pada hash :
TREE & BINARY TREE
Tree merupakan struktur data non-linear yang mewakili hubungan hierarkis di antara objek data, dan dode di tree tidak perlu disimpan secara berdekatan dan dapat disimpan di mana saja dan dihubungkan oleh pointer.
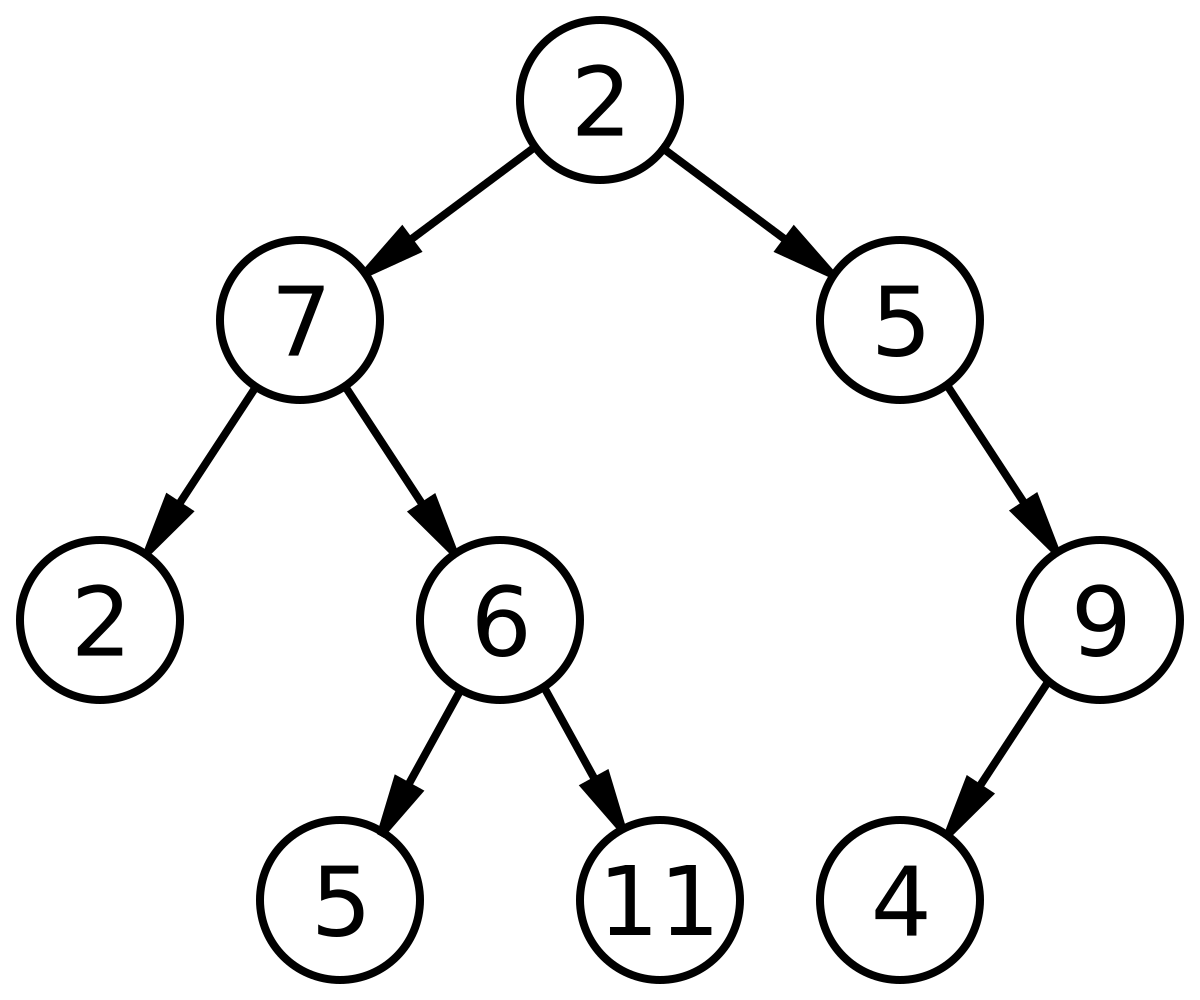
Sedangkan, Binary tree adalah suatu tree dengan syarat bahawa tiap node (simpul) hanya boleh memiliki maksimal dua subtree dan kedua subtree tersebut harus terpisah. Tiap node dalam binary tree boleh memiliki paling banyak dua child (anak simpul), secara khusus anaknya dinamakan kiri dan kanan. Binary tree dapat juga disimpan sebagai struktur data implisit dalam array, dan jika pohon tersebut merupakan sebuah pohon biner lengkap, metode ini tidak boros tempat.
Jenis-jenis Binary tree :
Kunjungan pada Binary tree (Prefix, Infix, Postfix)
1. Kunjungan secara preorder (Depth First Order) -> Prefix, mempunyai urutan :
a. Cetak isi simpul yang dikunjungi ( simpul akar ),
b. Kunjungi cabang kiri,
c. Kunjungi cabang kanan.


2. Kunjungan secara inorder ( symetric order) -> Infix, mempunyai urutan :
a. Kunjungi cabang kiri,
b. Cetak isi simpul yang dikunjungi (simpul akar),
c. Kunjungi cabang kanan.



merupakan metode untuk menyimpan data dalam sebuah array agar penyimpanan data, pencarian data, penambahan data, dan penghapusan data dapat dilakukan dengan cepat. Ide dasarnya adalah menghitung posisi recordyang dicari dalam array, bukan membandingkan record dengan isi pada array. Fungsi yang mengembalikan nilai atau kunci disebut fungsi hash (hashfunction) dan array yang digunakan disebut tabel hash (hash table). Hash tablemenggunakan struktur data array asosiatif yang mengasosiasikan recorddengan sebuah field kunci unik berupa bilangan (hash) yang merupakan representasi dari record tersebut.
Function-function yang terdapat pada hash :
- Mid-square
merupakan teknik hashing yang di mana kunci unik dihasilkan. Dalam teknik ini, nilai benih diambil dan dikuadratkan. Kemudian, beberapa digit dari tengah diekstraksi. Angka-angka yang diekstrak ini membentuk angka yang diambil sebagai benih baru. Teknik ini dapat menghasilkan kunci dengan keacakan tinggi jika nilai benih yang cukup besar diambil. Namun, itu memiliki batasan.
contoh : key=4765, dikuadratkan = 22705225, mid= 7052. - DivisionInti dari fungsi ini adalah membagi dan sisa pembagian nilai key field dijadikan alamat relatifnya. Tujuan dari fungsi ini adalah agar alamat yang akan digunakan bisa berbeda sekecil mungkin (menghemat memori) dan menghindari benturan yang bakal terjadi.Ada juga perhitungan faktor muat (load factor) yaitu jika kita memiliki record yang akan disimpan ke dalam memori, maka setidaknya kita menyediakan memori yang kapasitasnya lebih dari jumlah record tersebut.
contoh : ukuran tabel= 11, nilai 68 -> (68 mod 11) + 1 = 2 + 1 = 3 ; simpan 68 dilokasi 3. - FoldingTeknik ini digunakan untuk mendapatkan alamat relatif, nilai key dibagi menjadi beberapa bagian, setiap bagian (kecuali bagian terakhir) mempunyai jumlah digit yang sama dengan alamat relatif. Bagian-bagian ini kemudian dilipat (seperti kertas) dan dijumlah. Hasilnya, digit yang tertinggi dibuang (bila diperlukan).
contoh : 123456 -> 123+456 = 777; simpan 123456 dilokasi 777 - Digit Extraction
Teknik ini digunakan untuk memilih digit untuk diestrak dari key, yang akan digunakan sebagi alamat.
Contoh 14568 -> ambil digit ke 1,3,5 -> alamat = 158. - Rotating Hash
Teknik hashing yang membaca nilai asli dari belakang untuk dijadikan sebagai alamatnya.
contoh : 123456 -> alamat = 654321.
Collision
Merupakan peristiwa yang terjadi ketika ada 2 atau lebih kunci yang menghasilkan hash code yang sama (berebut dalam satu sel yang sama).
Merupakan peristiwa yang terjadi ketika ada 2 atau lebih kunci yang menghasilkan hash code yang sama (berebut dalam satu sel yang sama).
cara-cara yang dapat digunakan untuk mengatasi Collision :
Hashing benar-benar mendasar dalam penciptaan teknologi blockchain. Jika seseorang ingin memahami apa itu blockchain, mereka pasti harus mengerti apa artinya hashing. Karena hashing dapat menghasilkan
contoh salah satu implementasi Hash pada Blockchain adalah SHA256, karena dalam kasus SHA-256 , tidak peduli seberapa besar atau kecil input Anda, output akan selalu memiliki panjang 256-bit tetap. Ini menjadi penting ketika Anda berurusan dengan sejumlah besar data dan transaksi. Jadi pada dasarnya, alih-alih mengingat input data yang bisa jadi besar, Anda bisa mengingat hash dan terus melacak. Sebelum kita melangkah lebih jauh, kita perlu terlebih dahulu melihat berbagai properti fungsi hashing dan bagaimana mereka diimplementasikan di blockchain.4
- Linear Probing
metode yang digunakan untuk mencari sel yang kosong di bawah tempat terjadinya Collision. - Chaining
metode yang membuat rantai pada masing-masing sel, jadi ketika terjadi Collision pada salah satu sel, maka sel tersebut akan ditinggalkan.
contoh salah satu implementasi Hash pada Blockchain adalah SHA256, karena dalam kasus SHA-256 , tidak peduli seberapa besar atau kecil input Anda, output akan selalu memiliki panjang 256-bit tetap. Ini menjadi penting ketika Anda berurusan dengan sejumlah besar data dan transaksi. Jadi pada dasarnya, alih-alih mengingat input data yang bisa jadi besar, Anda bisa mengingat hash dan terus melacak. Sebelum kita melangkah lebih jauh, kita perlu terlebih dahulu melihat berbagai properti fungsi hashing dan bagaimana mereka diimplementasikan di blockchain.4
TREE & BINARY TREE
Tree merupakan struktur data non-linear yang mewakili hubungan hierarkis di antara objek data, dan dode di tree tidak perlu disimpan secara berdekatan dan dapat disimpan di mana saja dan dihubungkan oleh pointer.

Sedangkan, Binary tree adalah suatu tree dengan syarat bahawa tiap node (simpul) hanya boleh memiliki maksimal dua subtree dan kedua subtree tersebut harus terpisah. Tiap node dalam binary tree boleh memiliki paling banyak dua child (anak simpul), secara khusus anaknya dinamakan kiri dan kanan. Binary tree dapat juga disimpan sebagai struktur data implisit dalam array, dan jika pohon tersebut merupakan sebuah pohon biner lengkap, metode ini tidak boros tempat.
Jenis-jenis Binary tree :
- Full Binary Tree
Binary Tree yang tiap nodenya (kecuali leaf) memiliki dua child dan tiap subtree harus mempunyai panjang path yang sama. - Complete Binary Tree
Setiap subtree boleh memiliki panjang path yang berbeda. Node kecuali leaf memiliki 0 atau 2 child. - Skewed Binary Tree
Binary Tree yang semua nodenya (kecuali leaf) hanya memiliki satu child. - Similer Binary Tree
Dua pohon yang memiliki struktur yang sama tetapi informasinya berbeda. - Ekuivalent Binary Tree
Dua pohon yang memiliki struktur dan informasi yang sama.
1. Kunjungan secara preorder (Depth First Order) -> Prefix, mempunyai urutan :
a. Cetak isi simpul yang dikunjungi ( simpul akar ),
b. Kunjungi cabang kiri,
c. Kunjungi cabang kanan.
2. Kunjungan secara inorder ( symetric order) -> Infix, mempunyai urutan :
a. Kunjungi cabang kiri,
b. Cetak isi simpul yang dikunjungi (simpul akar),
c. Kunjungi cabang kanan.
3. Kunjungan secara postorder, mempunyai urutan :
a. Kunjungi cabang kiri,
b. Kunjungi cabang kanan,
c. Cetak isi simpul yang dikunjungi ( simpul akar ).

a. Kunjungi cabang kiri,
b. Kunjungi cabang kanan,
c. Cetak isi simpul yang dikunjungi ( simpul akar ).
Sumber : https://arisistemberkas.blogspot.com/2018/10/teknik-hashing.html
https://www.ilmuhacking.com/web-security/hashtable-collision-dos/
https://selembardigital.com/apa-itu-hashing-di-bawah-tudung-blockchain/
http://new-funday.blogspot.com/2012/12/struktur-data-tree-dan-penjelasaanya.html
http://firmanatduhri.blogspot.com/2015/03/pengertian-tree-dalam-bahasa-pemrograman.html
PPT Bimay
https://www.ilmuhacking.com/web-security/hashtable-collision-dos/
https://selembardigital.com/apa-itu-hashing-di-bawah-tudung-blockchain/
http://new-funday.blogspot.com/2012/12/struktur-data-tree-dan-penjelasaanya.html
http://firmanatduhri.blogspot.com/2015/03/pengertian-tree-dalam-bahasa-pemrograman.html
PPT Bimay
Binary Search Tree (BST)
merupakan sebuah konsep penyimpanan data, dimana data disimpan dalam bentuk tree yang setiap node dapat memiliki anak maksimal 2 node. Selain itu, terdapat juga aturan dimana anak kiri dari parent selalu memiliki nilai lebih kecil dari nilai parent dan anak kanan selalu memiliki nilai lebih besar dari parent.
Ciri-ciri BST :








merupakan sebuah konsep penyimpanan data, dimana data disimpan dalam bentuk tree yang setiap node dapat memiliki anak maksimal 2 node. Selain itu, terdapat juga aturan dimana anak kiri dari parent selalu memiliki nilai lebih kecil dari nilai parent dan anak kanan selalu memiliki nilai lebih besar dari parent.
Ciri-ciri BST :
- Setiap node mempunyai value dan tidak ada value yang double
- value yang ada di kiri tree lebih kecil dari rootnya
- value yang ada di kanan tree lebih besar dari rootnya
- kiri dan kanan tree bisa menjadi root lagi atau bisa mempunya child jadi BST ini memiliki sifat ( rekrusif )
Insert pada BST
- Dimulai dari root
- jika x lebih kecil dari node value(key) kemudian cek dengan sub-tree sebelah kiri lakukan pengecekan secara berulang ( rekrusif )
- jika x lebih besar dari node value(key) kemudian cek dengan sub-tree sebelah kanan lakukan pengecekan secara berulang ( rekrusif )
- Ulangi sampai menemukan node yang kosong untuk memasukan value X ( X akan selalu berada di paling bawah biasa di sebut Leaf atau daun )
deklarasi struct

function yang digunakan untuk membuat node baru

function untuk push(insert) -> single LL

function untuk push(insert) -> double LL

Delete pada BST
- Jika value yang ingin dihapus adalah Leaf(Daun) atau paling bawah , langsung delete
- Jika value yang akan dihapus mempunyai satu anak, hapus nodenya dan gabungkan anaknya ke parent value yang dihapus
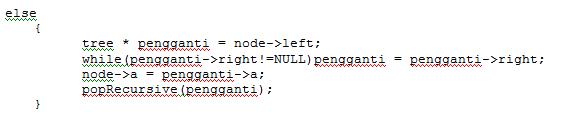
- jika value yang akan di hapus adalah node yang memiliki 2 anak , maka ada 2 cara , kita bisa cari dari left sub-tree anak kanan paling terakhir(leaf) (kiri,kanan) atau dengan cari dari right sub tree anak kiri paling terakhir(leaf) (kanan,kiri)
pada tahap Delete pada BST diperlukan fungsi search yang digunakan untuk mencari sebuah node dengan nilai tertentu. Kemudian fungsi ini akan mengembalikan nilai berupa node yang ditemukan atau NULL jika nilai yang dicari tidak ditemukan.

Case 1

Case 2
code ini digunakan ketika hanya tersisa anak kiri.

code ini digunakan ketika hanya tersisa anak kanan.

Case 3
AVL TREE
Avl tree merupakan BST yang telah diseimbangkan dengan perbedaan tinggi/ level maksimal 1 antara subtree kiri dan subtree kanan.
Contoh AVL :
Insert pada AVL Tree
Sebenarnya insert pada AVL Tree sama dengan insert pada BST, tetapi untuk tetap menjaga keseimbangan tree akan ada pemeriksaan peberdaan tinggi pada subtree kanan dan subtree kiri, jika perbedaannya lebih dari 1 tingkat, maka akan dilakukan perubahan pada node dengan rotasi-rotasi tertentu, Sehingga insert pada AVL Tree dibagi menjadi 2 macam :
- Single Rotation
Single rotation akan digunakan apabila jalur dari node yang bermasalah sampai porosnya itu lurus/tidak berbelok.
Konsep Single Rotation :
2. Double Rotation
Double rotation akan digunakan apbila jalur dari node yang bermasalah sampai porosnya itu
berbelok.
Konsep Double Rotation :
Double rotation akan digunakan apbila jalur dari node yang bermasalah sampai porosnya itu
berbelok.
Konsep Double Rotation :
Delete pada AVL Tree
Untuk delete pada AVL Tree hampir sama dengan Delete pada BST, tapi karena untuk menghapus node juga dapat menyebabkan tree menjadi tidak seimbang, jadi untuk itu pada Delete juga digunakan konsep Single Rotation dan Double Rotation.
Contoh :
Sumber :
http://dinda-dinho.blogspot.com/2013/06/pengertian-dan-konsep-avl-tree.html
PPT Binus AVL Tree
Heap and Tries
Heap
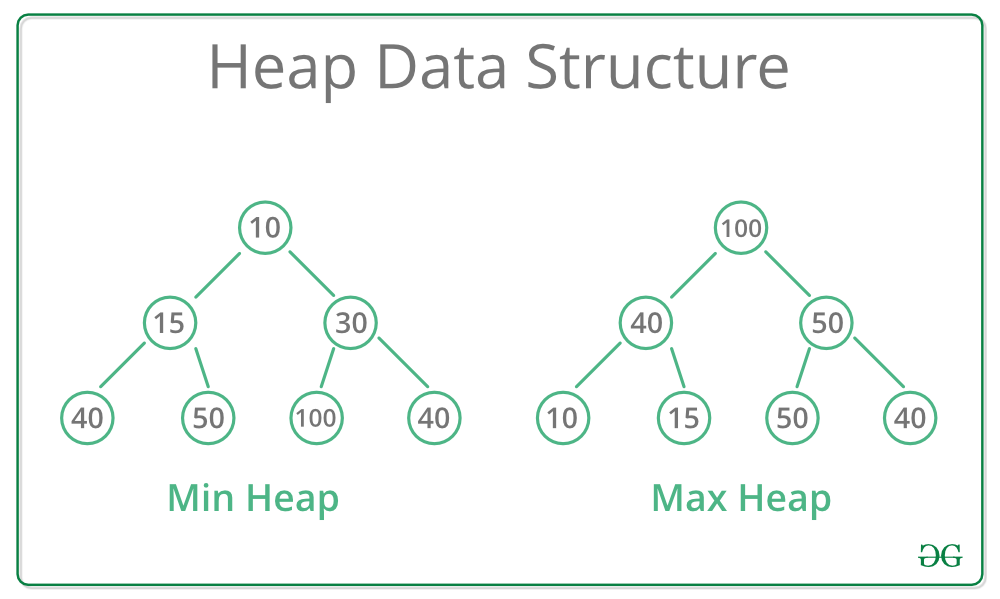
Heap merupakan complete binary tree.
Heap terdiri dari :
- Min Heap = pada heap ini root merupakan node terkecil, dan leafnya merupakan node terbesar, oleh karena itu setiap node lebih kecil dibandingkan childnya masing-masing.
2. Max Heap = pada heap ini root merupakan node terbesar, dan leafnya merupakan node terkecil, oleh karena itu setiap node lebih besar dibandingkan childnya masing-masing.
3. Min-max Heap = pada heap ini, min heap terdapat pada level ganjil dan max heap terdapat di level genap.
Insert pada Heap
1. Min Heap = insert pada heap ini, node selalu berurutan dari level paling rendah dan urutannya dari left ke right, dan lakukan pengecekan apakah parentnya lebih kecil atau lebih besar, jika lebih besar lakukan pertukaran(up heap), lakukan secara rekursif.
2. Max Heap = insert pada heap ini, node selalu berurutan dari level paling rendah dan urutannya dari left ke right, dan lakukan pengecekan apakah parentnya lebih kecil atau lebih besar, jika lebih kecil lakukan pertukaran(up heap), lakukan secara rekursif.
3. Min-max Heap = insert pada heap ini, node selalu berurutan dari level paling rendah dan urutannya dari left ke right, dan lakukan pengecekan apakah parent dan grandparentnya lakukan secara rekursif.
Delete pada Heap
1. Min Heap : pada heap ini, node yang dihapus selalu root karena root merupakan node yang paling kecil, setelah itu root diganti dengan node paling akhir, lalu lakukan pengecekan min heap seperti biasa secara rekursif.
2. Max heap = delete pada heap ini kurang lebih sama dengan min heap, hanya saja pengecekannya max heap dan dilakukan secara rekursif.
3. Min-max Heap = pada tahap ini, node dihapus juga selalu root, lalu lakukan downheap sesuai level node, dan lakukan pengecekan pada child dan grand child, dilakukan secara rekursif.
Implementasi heap pada linke list contohnya Priority Queue.
Dan untuk implementasi heap menggunakan array :
1. Biasanya index array pada heap dimulai dari 1.
2. Rumus untuk mencari Parent = index/2
Dan untuk implementasi heap menggunakan array :
1. Biasanya index array pada heap dimulai dari 1.
2. Rumus untuk mencari Parent = index/2
3. Rumus untuk mencari Left-child = 2*index
4. Rumus untuk mencari Right-child = 2*index+1
Pengaplikasian Heap
Heap Sort = untuk Min heap -> ascending dan untuk Max heap -> descending.
konsep heap sort sama seperti delete pada heap, tapi nilai yang didelete disimpan untuk dijasikan sebagai hasil sorting.
konsep heap sort sama seperti delete pada heap, tapi nilai yang didelete disimpan untuk dijasikan sebagai hasil sorting.
Tries
Tries merupakan tree yang digunakan untuk menyimpan array asosiatif.
1. Node pada tries merupakan character.
1. Node pada tries merupakan character.
2. Root pada tries biasnya kosong, agar pembentukan kata menjadi lebih fleksibel
Sumber :
PPT Binus Maya (Heap and Tries)
http://gabrielyakub.blogspot.com/2016/05/pertemuan-8-heap-tries-hashing.html
https://www.geeksforgeeks.org/heap-data-structure/
PPT Binus Maya (Heap and Tries)
http://gabrielyakub.blogspot.com/2016/05/pertemuan-8-heap-tries-hashing.html
https://www.geeksforgeeks.org/heap-data-structure/


















Comments
Post a Comment