Heap and Tries

Heap and Tries

Heap

Heap merupakan complete binary tree.

Heap terdiri dari :

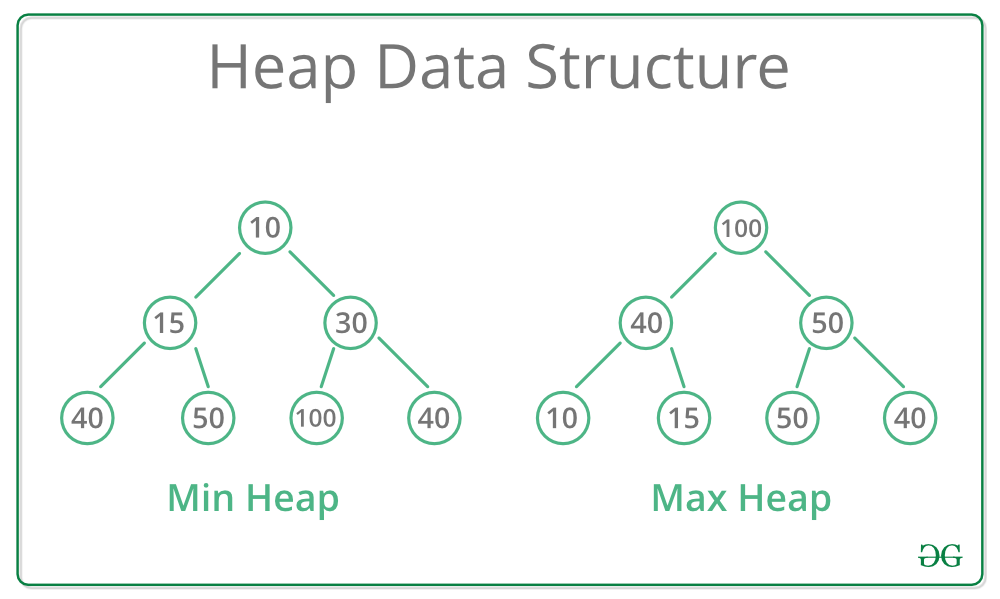
1. Min Heap = pada heap ini root merupakan node terkecil, dan leafnya merupakan node terbesar, oleh karena itu setiap node lebih kecil dibandingkan childnya masing-masing.

   2. Max Heap = pada heap ini root merupakan node terbesar, dan leafnya merupakan node                         terkecil, oleh karena itu setiap node lebih besar  dibandingkan childnya masing-masing.

  3. Min-max Heap = pada heap ini, min heap terdapat pada level ganjil dan max heap terdapat di              level genap.

Insert pada Heap

1. Min Heap = insert pada heap ini, node selalu berurutan dari level paling rendah dan urutannya dari left ke right, dan lakukan pengecekan apakah parentnya lebih kecil atau lebih besar, jika lebih besar lakukan pertukaran(up heap), lakukan secara rekursif.

2. Max Heap = insert pada heap ini, node selalu berurutan dari level paling rendah dan urutannya dari left ke right, dan lakukan pengecekan apakah parentnya lebih kecil atau lebih besar, jika lebih kecil lakukan pertukaran(up heap), lakukan secara rekursif.

3. Min-max Heap = insert pada heap ini, node selalu berurutan dari level paling rendah dan urutannya dari left ke right, dan lakukan pengecekan apakah parent dan grandparentnya lakukan secara rekursif.

Delete pada Heap

1. Min Heap : pada heap ini, node yang dihapus selalu root karena root merupakan node yang paling kecil, setelah itu root diganti dengan node paling akhir, lalu lakukan pengecekan min heap seperti biasa secara rekursif.

2. Max heap = delete pada heap ini kurang lebih sama dengan min heap, hanya saja pengecekannya max heap dan dilakukan secara rekursif.

3. Min-max Heap =  pada tahap ini, node dihapus juga selalu root, lalu lakukan downheap sesuai level node, dan lakukan pengecekan pada child dan grand child, dilakukan secara rekursif.

Implementasi Heap
Heap biasanya diimplementasikan  dengan array maupun  dengna linked list.

Implementasi heap pada linke list contohnya Priority Queue.

Dan untuk implementasi heap menggunakan array :
1. Biasanya index array pada heap dimulai dari 1.
2. Rumus untuk mencari Parent = index/2

3. Rumus untuk mencari Left-child = 2*index

4. Rumus untuk mencari Right-child = 2*index+1

Pengaplikasian Heap

Heap Sort = untuk Min heap -> ascending dan untuk Max heap -> descending.
konsep heap sort sama seperti delete pada heap, tapi nilai yang didelete disimpan untuk dijasikan sebagai  hasil sorting.

Tries

Tries merupakan tree yang digunakan untuk menyimpan array asosiatif.
1. Node pada tries merupakan character.

2. Root pada tries biasnya kosong, agar pembentukan kata menjadi lebih fleksibel

Sumber :
PPT Binus Maya (Heap and Tries)
http://gabrielyakub.blogspot.com/2016/05/pertemuan-8-heap-tries-hashing.html
https://www.geeksforgeeks.org/heap-data-structure/